A Spline Theory of Deep Learning 阅读笔记

机器学习 论文笔记 样条理论 spline theory
发布日期:   2023-07-22
更新日期:   2023-08-06
文章字数:   4k
阅读时长:   15 分
阅读次数:  

A Spline Theory of Deep Learning

Metadata

  • Type: ConferencePaper
  • Title: A Spline Theory of Deep Learning,
  • Author: Balestriero, Randall; baraniuk,,
  • Year: 2018 ;
    • Pages: 374-383
    • Publisher: PMLR,

Abstract

We build a rigorous bridge between deep networks (DNs) and approximation theory via spline functions and operators. Our key result is that a large class of DNs can be written as a composition of max-affine spline operators (MASOs), which provide a powerful portal through which to view and analyze their inner workings. For instance, conditioned on the input signal, the output of a MASO DN can be written as a simple affine transformation of the input. This implies that a DN constructs a set of signal-dependent, class-specific templates against which the signal is compared via a simple inner product; we explore the links to the classical theory of optimal classification via matched filters and the effects of data memorization. Going further, we propose a simple penalty term that can be added to the cost function of any DN learning algorithm to force the templates to be orthogonal with each other; this leads to significantly improved classification performance and reduced overfitting with no change to the DN architecture. The spline partition of the input signal space opens up a new geometric avenue to study how DNs organize signals in a hierarchical fashion. As an application, we develop and validate a new distance metric for signals that quantifies the difference between their partition encodings.

我们通过样条函数和运算符在深度网络（DNs）和逼近理论之间建立了严谨的桥梁。我们的关键结果是，大部分的深度网络可以被写成最大仿射样条运算符（MASOs）的组合形式，这为我们观察和分析其内部工作提供了强大的途径。例如，对于给定的输入信号，MASO DN的输出可以被表示为输入的简单仿射变换。这意味着DN构建了一组依赖于信号的、类别特定的模板，通过简单的内积与信号进行比较；我们探索了与经典的通过匹配滤波器进行最优分类理论的联系以及数据记忆的影响。进一步地，我们提出了一个简单的惩罚项，可以添加到任何DN学习算法的损失函数中，强制模板彼此正交；这将显著提高分类性能，并减少过拟合，而无需改变DN的架构。输入信号空间的样条分区为我们研究DN如何以分层方式组织信号提供了一条新的几何途径。作为一个应用，我们开发并验证了一种用于信号的新的距离度量，用于量化它们分区编码之间的差异。

Introduction

深度学习极大地提升了我们解决各种困难的机器学习和信号处理问题的能力。当今的机器学习领域被深度（神经）网络（DNs）所主导，它们由大量简单参数化的线性和非线性变换组成。最近普遍的情况是将深度网络作为黑盒子插入应用程序中，在大量训练数据上进行训练，然后在性能上显著超越传统方法。

尽管取得了实证方面的进展，但深度学习能够如此出色地工作的确切机制仍然相对不太清楚，给整个领域增添了一丝神秘感。目前对建立严格的数学框架的努力大致可分为五个阵营：(i) 探测和测量深度网络以可视化其内部工作机制 (Zeiler & Fergus, 2014)；(ii) 分析深度网络的性质，如表达能力 (Cohen et al., 2016)、损失曲面几何 (Lu & Kawaguchi, 2017; Soudry & Hoffer, 2017)、干扰管理 (Soatto & Chiuso, 2016)、稀疏化 (Papyan et al., 2017) 和泛化能力；(iii) 新的数学框架，与深度网络有一些（但不是全部）共同特征 (Bruna & Mallat, 2013)；(iv) 可以导出特定深度网络的概率生成模型 (Arora et al., 2013; Patel et al., 2016)；以及 (v) 信息理论界限 (Tishby & Zaslavsky, 2015)。

在本文中，我们通过样条函数和运算符在深度网络（DNs）和逼近理论之间建立了严谨的桥梁。我们证明了一大类DNs，包括卷积神经网络（CNNs）（LeCun，1998）、残差网络（ResNets）（He等，2016；Targ等，2016）、跳跃连接网络（Srivastava等，2015）、全连接网络（Pal＆Mitra，1992）、循环神经网络（RNNs）（Graves，2013）等，可以被写成样条运算符的形式。特别是当这些网络采用当前的标准实践分段仿射凸非线性（例如ReLU，最大池化等）时，它们可以被写成最大仿射样条运算符（MASOs）的组合形式（Magnani＆Boyd，2009；Hannah＆Dunson，2013）。我们在这里重点关注这样的非线性函数，但请注意，我们的框架也适用于非分段仿射非线性函数，通过标准的逼近论证可以实现。

最大仿射样条连接为使用逼近理论和函数分析工具来观察和分析深度网络内部工作提供了一个强大的途径。以下是我们的主要贡献的总结：

a) 我们证明了大部分深度网络可以被写成最大仿射样条运算符（MASOs）的组合形式，由此可立即得出结论：在给定输入信号的条件下，深度网络的输出是输入的简单仿射变换。在第4节中，我们通过推导卷积神经网络（CNN）的输入/输出映射的闭式表达式来进行说明。
b) 仿射映射公式使我们能够将MASO深度网络解释为构建了一组依赖于信号的、类别特定的模板，通过简单的内积与信号进行比较。在第5节中，我们将深度网络与经典的通过匹配滤波器进行最优分类理论直接相关联，并提供了关于数据记忆效应的见解（Zhang等，2016）。
c) 我们提出了一个简单的惩罚项，可以添加到任何深度网络学习算法的损失函数中，以强制模板彼此正交。在第6节中，我们展示了这将显著提高在标准测试数据集（如CIFAR100）上的分类性能，并减少过拟合，而无需对深度网络的架构进行任何改变。
d) MASO所引发的输入空间的分区将深度网络与矢量量化（VQ）和K均值聚类理论联系起来，为研究深度网络如何以分层方式对信号进行聚类和组织提供了一条新的几何途径。第7节研究了MASO分区的性质。
e) 利用事实：如果两个信号位于相同的MASO分区区域中，那么深度网络将他们视为相似的。我们在第7.3节中开发了一种新的信号距离，用于衡量它们分区编码之间的差异。该距离可以通过反向传播轻松计算。

补充材料（SM）中的一些附录包含了数学设置和证明。关于这些内容的大幅扩展及众多新结果的详细说明可在（Balestriero＆Baraniuk，2018）中找到。

Background / Problem Statement

神经网络基础

深度神经网络是一种算子，该算子将输入的信号$x\in \mathbb R^D$映射到预测值$\hat{y} \in \mathbb R^C$ ，即$f_{\Theta}:\mathbb R^D \to \mathbb R^C$。所有的神经网络可以写作是L个中间映射的组合：

其中$\Theta=\left\{\theta^{(1)},\ldots,\theta^{(L)}\right\}$是每一层的网络参数集合。整体上来说，这种映射的组合是非线性且不可交换的。

样条算子基础

逼近论是研究如何以及多好的函数可以最好地用更简单的函数来逼近的理论。这篇文章主要讨论仿射样条（线性样条），即每一段都用线性函数去拟合。

举例：样条函数
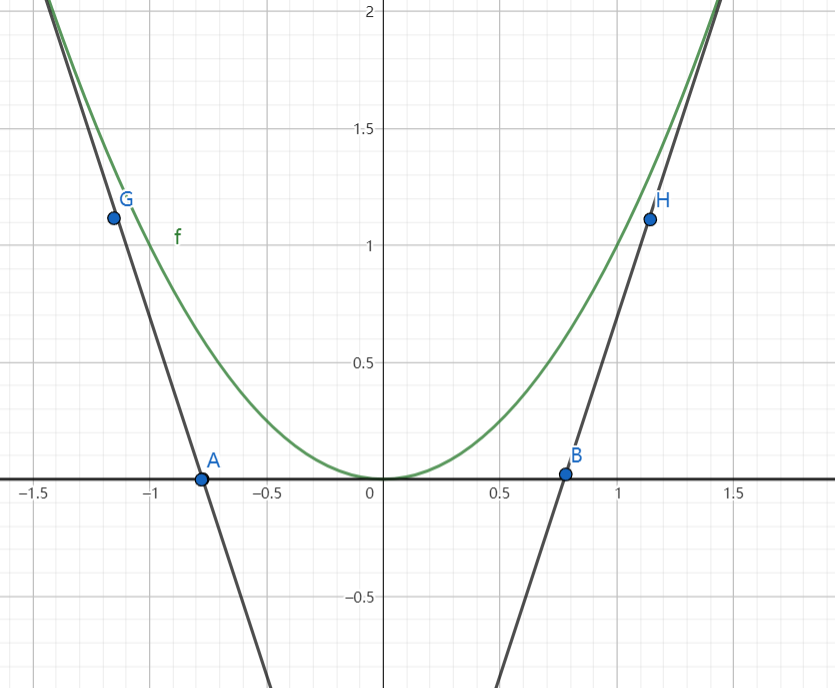
在逼近理论中，样条函数是一种使用分段的多项式函数来逼近复杂函数的工具。比如下图的$y=x^2$曲线，我们可以把x轴分割为三段，每一段分别用AG、AB、BH三条直线去拟合。下面所示的样条函数有两类需要优化的参数：1. 分段位置 2. 每一段分别用什么函数去拟合。
img

多元仿射样条(Multivariate Affine Splines)：考虑对域$\mathbb R^D$的一个分割$\Omega=\{\omega_1,\dots,\omega_R\}$，和一系列的本地映射$\Phi=\{\phi_{1},\ldots,\phi_{R}\}$。本地映射和子域一一对应，并将子域中的点$x\in \omega_r$映射到$\mathbb R$。形式上，$\phi_r(\boldsymbol{x}):=\langle[\alpha]_{r,\cdot},\boldsymbol{x}\rangle+[\beta]_r$。其中$\alpha\in \mathbb R^{R\times D},\beta \in \mathbb R^R$。$[\alpha]_r$表示由$\alpha$的第r行组成的列向量。在此设定下，多元仿射样条的定义如下:

$\mathbf{1}(x\in \omega_r)$是一个指示函数，当满足括号里的条件时其值为1，否则为0。这样定义的样条是分段仿射且分段凸的。只有在R=1时，其为全局仿射和全局凸。我们称这种情况下的多元放射样条为退化样条。

最大仿射样条函数(Max-Affine Spline Functions)：用仿射函数进行逼近的主要挑战是我们需要同时优化样条参数$\alpha,\beta$和输入域的分割$\Omega$。但是，如果我们限制仿射样条为全局凸的，则这个仿射样条可以被写为最大仿射样条：

这种样条的一个非常有用的特点是它完全由它的参数$\alpha,\beta$决定，而不需要指定划分$\Omega$。

举例：最大仿射样条
还是上面的图。如果我们对仿射样条加以限制，使其为全局凸的，假设直线AG为$y=a_1x+b_1$，直线AB为$y=a_2x+b_2$，直线BH为$y=a_3x+b_3$ ，则该仿射样条可以写作：$y=MAX\{y=a_1x+b_1,y=a_2x+b_2,y=a_3x+b_3\}$。这种情况下，对参数$a_i,b_i$的改变同时会影响到分割$\Omega$。故只需要对$\alpha,\beta$进行优化。

最大仿射样条算子(Max-Affine Spline Operators)：是最大仿射样条函数的一种拓展，他会产生多元的输出。这种算子由K个最大仿射样条函数的拼接得到。一个由参数$A\in\mathbb R^{K\times R\times D}, B\in\mathbb R^{K\times R}$定义的MASO可以表示为：

最大仿射样条函数和算子关于每个输出维度始终是分段仿射和全局凸的(因此也是连续的)。反之，任何分段仿射和全局凸函数/算子都可以写成一个极大仿射样条。此外，利用标准的逼近论点，很容易证明一个MASO可以任意逼近任意在每个输出维数上是凸的(非线性)算子。

深度神经网络是仿射算子的组合

虽然MASO仅适用于逼近凸函数/算子，但我们现在展示了几乎所有现今的深度网络(DNs)都可以被写成MASO的复合形式，每一层都对应一个MASO。这样的复合在一般情况下是非凸的，因此可以逼近更广泛的函数/算子类别。有趣的是，在某些广泛条件下，这种复合仍然是分段仿射样条算子，从而为深度网络(DNs)提供了各种洞察力。

深度神经网络的算子是MASO

命题一：任意一个全连接算子 $f^{(l)}_W$是仿射算子，因此也是一个退化的MASO $S\Big[A_{\boldsymbol{W}}^{(\ell)},B_{\boldsymbol{W}}^{(\ell)}\Big],R=1.[A_{\boldsymbol{W}}^{(\ell)}]_{k,1,}.=\left[W^{(\ell)}\right]_{k},[B_{\boldsymbol{W}}^{(\ell)}]_{k,1}={\left[b_{\boldsymbol{W}}^{(\ell)}\right]}_{k}$。卷积层同理。

命题二：任意一个满足分段仿射且凸的激活函数是一个MASO $S\Big[A_\sigma^{(\ell)},B_\sigma^{(\ell)}\Big],R=2$。$\left[B_{\sigma}^{(\ell)}\right]_{k,1}=\left[B_{\sigma}^{(\ell)}\right]_{k,2}=0 \quad \forall k$.

对于ReLU：$\left[A_{\sigma}^{(\ell)}\right]_{k,1,\cdot}=0,\left[A_{\sigma}^{(\ell)}\right]_{k,2,\cdot}=e_k \quad \forall k$；

对于leaky ReLU：$\left[A_{\sigma}^{(\ell)}\right]_{k,1,\cdot}=\nu\boldsymbol{e}_{k},\left[A_{\sigma}^{(\ell)}\right]_{k,2,\cdot}=e_k \quad \forall k,v>0$；

对于绝对值函数：$\left[A_{\sigma}^{(\ell)}\right]_{k,1,\cdot}=-\boldsymbol{e}_{k},\left[A_{\sigma}^{(\ell)}\right]_{k,2,\cdot}=e_{k}\quad\forall k$

其中 $e_{k}$ 代表 $\mathbb R^{D^{(l)}}$ 第k个正交基向量。

命题三：任意一个满足分段仿射和凸的池化层都是一个MASO。

对于最大池化层， $R=\mathcal{R}_{k}$ (通常在所有输出维度上为常数).$\left[A_{\rho}^{(\ell)}\right]_{k,\cdot,\cdot}=\{e_{i},i\in\mathcal{R}_{k}\},\left[B_{\rho}^{(\ell)}\right]_{k,r}=0\forall k,r$。

平均池化层是一个退化的MASO(R=1), $\left[A_\rho^{(\ell)}\right]_{k,1,\cdot}=\frac1{(\mathcal{R}_k)}\sum_{i\in\mathcal{R}_k}e_i,\begin{bmatrix}B_{\rho}^{(\ell)}\end{bmatrix}_{k,1}=0\forall k.$

命题四：由全连接/卷积算子任意组合构造的DN接上一个激活或池化算子的网络是一个MASO $S[A^{(\ell)},B^{(\ell)}]$,表示为：

因此，许多深度网络(DNs)都可以归结为MASO的复合形式。论文在附录中对CNN、ResNet、跳跃连接网络、全连接网络和RNN等进行了证明。

定理一：由1至命题3中的任意全连接/卷积、激活和池化算子组成的深度网络（DN），是一个MASO的复合形式，等价于一个全局仿射样条算子。

需要注意的是，尽管定理1中所述的每个深度网络（DN）的层都是MASO，但多个层的复合形式不一定是MASO。事实上，MASO的复合仅在其所有组成算子（除了第一个算子）相对于它们各自的输出维度都是非减的情况下才仍然是MASO（Boyd＆Vandenberghe，2004）。有趣的是，ReLU和最大池化都是非减的，而leaky ReLU是严格递增的。导致复合层非凸性的罪魁祸首是全连接或卷积算子中的负项，这破坏了所需的非增性质。当这些罪魁祸首被排除时，DN就成为一个有趣的特例，因为它相对于其输入是凸的（Amos等人，2016），并且相对于其参数是多凸的（Xu＆Yin，2013）。
定理二：一个深度神经网络，它的第$2,\dots,L$层由具有非负权重（即$\boldsymbol{W}_{k,j}^{(\ell)}\geq0,\boldsymbol{C}_{k,j}^{(\ell)}\geq0;$）、非减、分段仿射和凸的全连接和卷积算子的任意组合构成，则这个网络是全局MASO，因此关于其每个输出维度也是全局凸的。

上述结果涉及使用凸的仿射算子的深度网络（DNs）。其他流行的非凸DN算子（例如sigmoid和arctan激活函数）可以被仿射样条算子任意接近逼近，但不能被MASO逼近。

DNs是信号相关的仿射变换。上述结果的一个共同主题是，对于由命题1至命题3中的全连接/卷积、激活和池化算子构建的深度网络（DNs），算子/层的输出$z^{(l)}(x)$总是输入x的一个信号相关的仿射函数。应用到x的特定仿射映射取决于它在RD中哪个样条分区中。

文章作者: wangxh
文章链接: https://blog.expecto.top/2023/07/22/a-spline-theory-of-deep-learning/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 wangxh !
机器学习 论文笔记 样条理论 spline theory
  目录