Can Neural Network Memorization Be Localized 阅读笔记

论文题目：Can Neural Network Memorization Be Localized
发表时间：2023
发表期刊/会议： ICML, CCF A

1. 内容简介

这篇文章通过实验讨论模型的记忆性是否可以被定位到网络的特定部分。有之前的工作认为主要是模型的最后几层具有记忆性，但本篇论文反驳了这个观点，并提出模型的记忆性来自于所有层的个别神经元。

2. 主要内容

2.1 问题设定

讨论模型的记忆性首先要明确什么是模型的记忆性。在论文intro部分写道 目前一种常见模型记忆性的定义是，如果把一个非典型（可能指离群点）样本从训练集中移除，模型对其预测标签产生了明显的变化（在训练集时预测正确，移除后预测错误），则认为模型对这个样本产生了记忆。但计算这一度量的开销较大，故许多研究使用错误标注样本来衡量记忆程度，因为模型必须记住这个样本才能正确预测。这篇论文同时探讨非典型的记忆化喝错误标注的记忆化。

Preliminaries:考虑一个d层的前馈神经网络$\mathcal F_d$，其参数为$\theta = (\theta_1,\dots,\theta_d)$。使用$z_l$表示第$l$层的激活输出，可以使用下式进行表达：

$$z_l = \mathcal F(z_{l-1};\theta_l)$$

使用$[z_l]_j$表示第j个神经元/通道。模型使用监督学习训练，数据集为$\mathcal S=\{x_i,y_i\}^n$，优化器为SGD。第t个epoch训练的结果为$\theta^t=\{\theta_1^t,\dots,\theta_d^t\}$

在带有标签噪声的实验中，论文随机改变了固定比例样本的标签。$\mathcal S=\mathcal S_c \cup \mathcal S_n$，其中c表示干净样本，n表示改变了标签的样本。

数据集和模型：数据集有CIFAR10，MNIST，SVHN。模型有ResNet-9，ResNet-50，ViT

2.2 梯度核算

在训练模型时，梯度更新公式为：

$$\theta_l^{t+1}=\theta^t_l-\eta \frac{d\mathcal L(\mathcal S,\mathcal F_d)}{d\theta_l}$$

梯度决定了如何更新模型的参数。如果一个知识被编码进模型参数，则梯度的大小就可以作为模型对该知识记忆潜力的表征。

2.2.1 分层范数贡献

为了获得干净样本和错误标注样本对梯度的贡献，论文使用$||d\mathcal L(\mathcal S_c,\mathcal F_d)||_2,||d\mathcal L(\mathcal S_n,\mathcal F_d)||_2$作为指标。使用每一层参数个数的算数平方根对其进行归一化。为了综合不同轮数或不同层的结果，使用平均值进行统计。

从下图可以看出不存在哪一层的错误标注样本（记忆样本，Noisy样本）比干净样本的贡献值更大。同时论文也观测到一个有趣的事实是即使错误标注样本只占10%，他们对梯度的贡献度和其它样本整体的贡献度几乎一样大。这表明即使不存在特定的哪一层记住了错误标注样本，他们也确实对模型的每一层产生了巨大影响，这也意味着错误标注样本的梯度范数比干净样本高一个数量级。

2.2.2 干净样本和错误标注样本的梯度相似度

上图展示的结果可以看到整体梯度值比单独的干净或错误标注样本小很多，这说明干净样本和噪声样本的梯度方向可能是相反的。论文对每一层每一个epoch里干净样本和错误标注样本的梯度平均值的余弦相似度进行计算。结果如下图。

可以看到干净样本和错误标注样本的余弦相似度非常小。但该实验暂时无法说明(1) 每个神经元是否存在梯度错位（2）这是一个只发生在宏观层级的现象。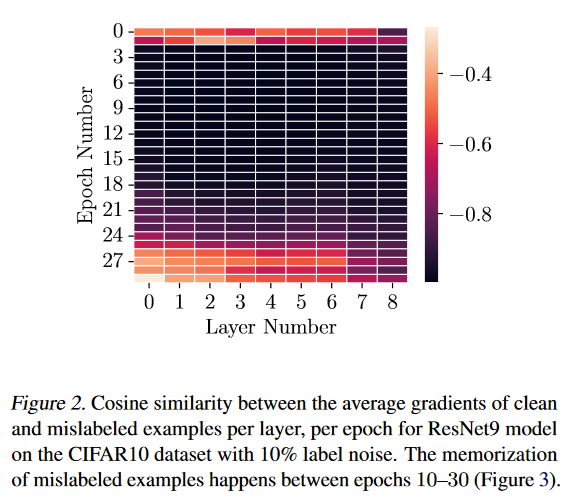

和图三（下图）的曲线对比可以发现错误标注样本被模型学习的主要阶段在第10-30轮。对于所有轮所有层大多数时间两种样本余弦相似度的值都低于-0.75。这表明对错误标注的样本进行过拟合可能不是一种良性的现象。

2.3 层的功能临界性

2.3.1 层回溯

对于一个已经训练T轮收敛的模型$\mathcal F_d$，参数是$(\theta_1^T,\dots.\theta_d^T)$，论文把模型某一层的参数回退到第t轮的checkpoint，对每一层都重复这个过程。接着利用模型训练集对模型性能进行测试。结果如下图（图三）所示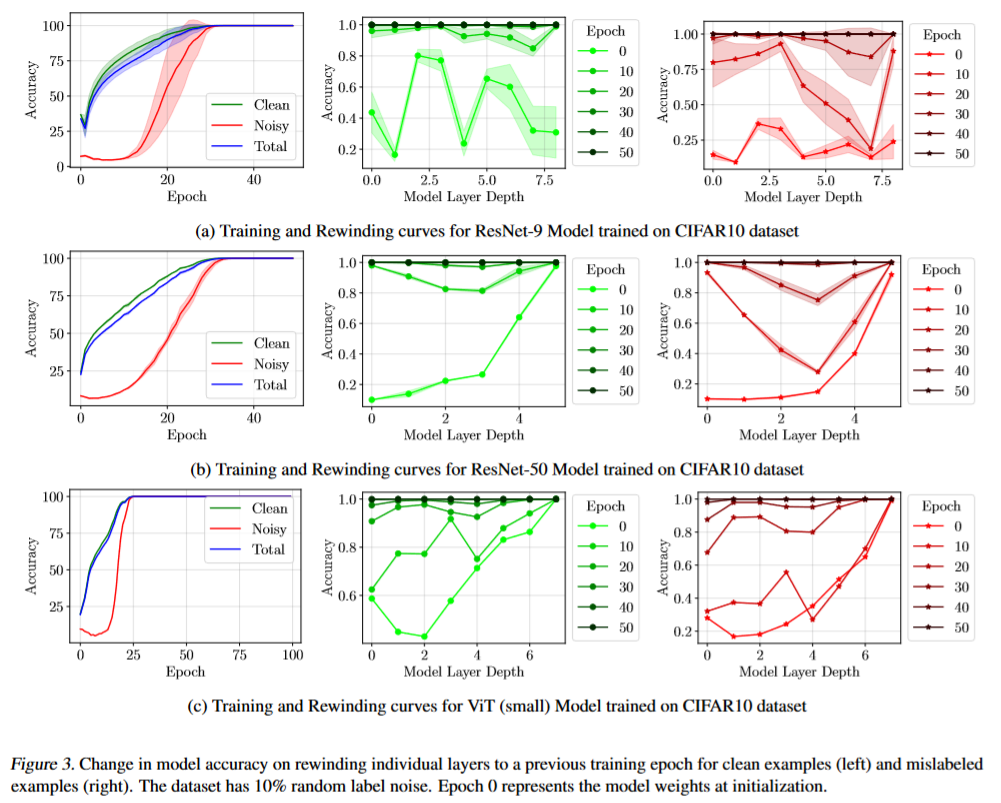

分析可知：

1. 对模型最后一层进行回溯造成的影响较少（绿线和红线末尾准确率都比较高）
2. （没看懂在说啥，感觉和图展示的不一样）If contrasted with learning dynamics of the memorized examples (Figure 3 (left)), we observe that the model accuracy on noisy examples stays below 20% until the 30th epoch. Despite this, rewinding individual model layers to a checkpoint before the 30th epoch does not reduce accuracy on memorized examples. This seemingly contradicts the hypothesis that memorization happens in the last (few) layer(s).
3. 不同模型记忆错误标注样本的关键层不同。

综合信息表明：

1. 模型的记忆性分布在不同的层里
2. 模型记忆性分布和问题相关
3. 记忆层与学习干净样本的关键层有一定重叠

2.3.2 层重训练

从上面的实验中注意到错误标注样本的关键层对干净样本同样重要。不同层固有的的学习速率可能是一个额外因素。为了进一步研究，论文将某一层回溯到初始状态后使用干净数据进行重训练。

对$\mathcal F_d$的第l层进行重新训练时，初始化参数如下：

$$\theta_{init}=(\theta_1^T,\dots,\theta_{l-1}^T,\theta_l^0,\theta_{l+1}^T,\dots,\theta^T_d)$$

使用单周期学习率调度对模型进行20轮训练，第10轮时学习率到达最大值0.1，其它层参数保持冻结。

下图结果表明，即使只使用干净样本训练单个层，它仍可以在没见过噪声样本的情况下对其进行准确预测。表明预测噪声样本的信息已经保存在其他层，该层对于噪声样本的记忆是冗余的。需要注意的是这个推导过程是单向的，即如果预测效果不好也不能说明该层对记忆至关重要，因为模型优化可能有多个最优解，可能由于优化路径不同导致结果的变化。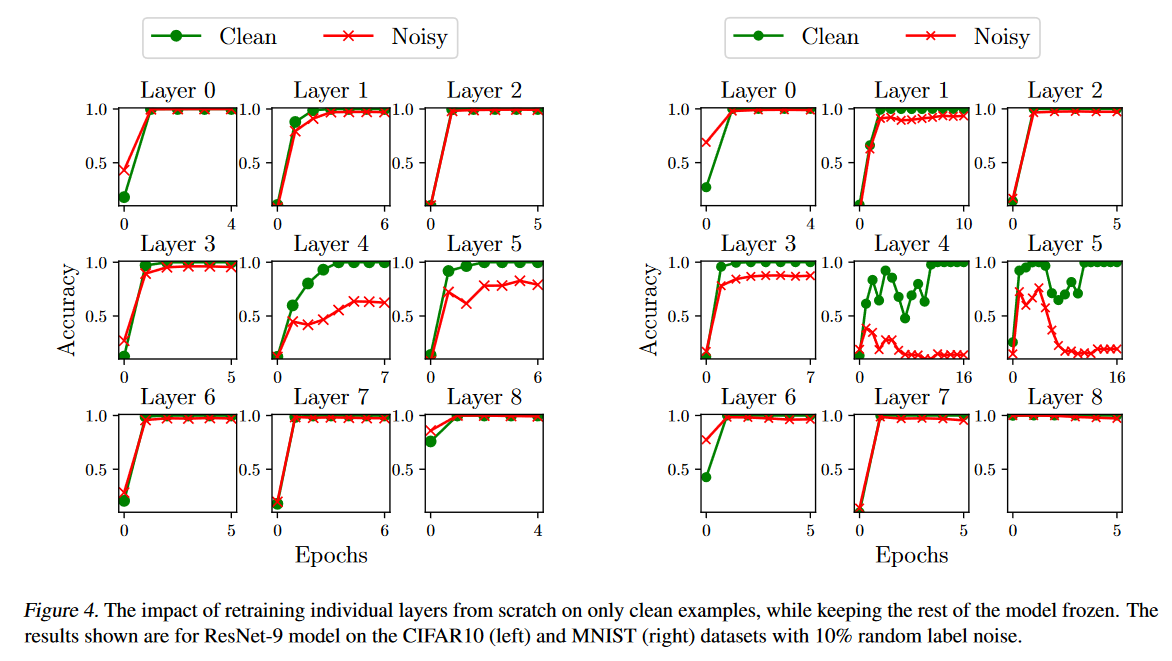

2.4 单个神经元的记忆性

2.4.1 预测一个样本需要多少个神经元？

论文利用基于梯度的贪心搜索来迭代的找到给定候选样本上的预测的最重要的神经元。
具体方法为：

1. 线性层：将某个神经元的权重置0
2. 卷积层：将某一层的整个通道置0

为了更鲁棒的找到某个样本的重要神经元，论文采用如下的方法（按我的理解是通过修改参数翻转该样本的预测结果，然后记录翻转过程中神经元的变化）：

1. 保持预测结果不变：最小化训练集随机batch的损失，最大化待翻转样本的损失
2. 添加高斯噪声：在输入上添加噪声，并基于五组噪声样本预测结果的均值进行搜索（避免产生对抗样本）
   模型记为$\overline{\mathcal {F_d}}$对于每个样本，上述过程需要独立的执行30次，然后平均30次的执行结果。寻找重要神经元的优化目标可以形式化为 ： $$\left[z_l\right]_j^*=\arg \max _{l, j}\left[\nabla_{\theta_l}\left(\ell\left(\overline{\mathcal{F}_d}\left(\mathbf{x}_i\right), \mathbf{y}_i\right)-\frac{1}{n} \mathcal{L}\left(\mathcal{S}, \overline{\mathcal{F}_d}\right)\right)\right]_j$$

在卷积层的情况下，$[z_l]_j​$代表的是整个通道的激活值；在线性层的情况下，代表的是单个神经元的激活值。我们将该激活值置零，然后继续前向传播，直至该样本的预测翻转到错误类别。这一过程将迭代进行，直到样本的预测发生翻转。记录屏蔽的神经元数量。

意思是找到一个神经元，使得将该神经元屏蔽（激活后的值置为0）后argmax里面的优化项值最大。优化项的含义是该样本的损失和训练集平均损失的差值在神经元上的梯度值。如果屏蔽了这个神经元后样本标签没有发生偏转则继续执行此过程。

实验结果如下图所示。可以发现干净样本需要置0 的神经元个数显著多于噪声样本。这说明只有极少数神经元负责记忆错误标注样本（噪声样本、记忆样本）。超过90%的错误标注样本需要小于10个神经元。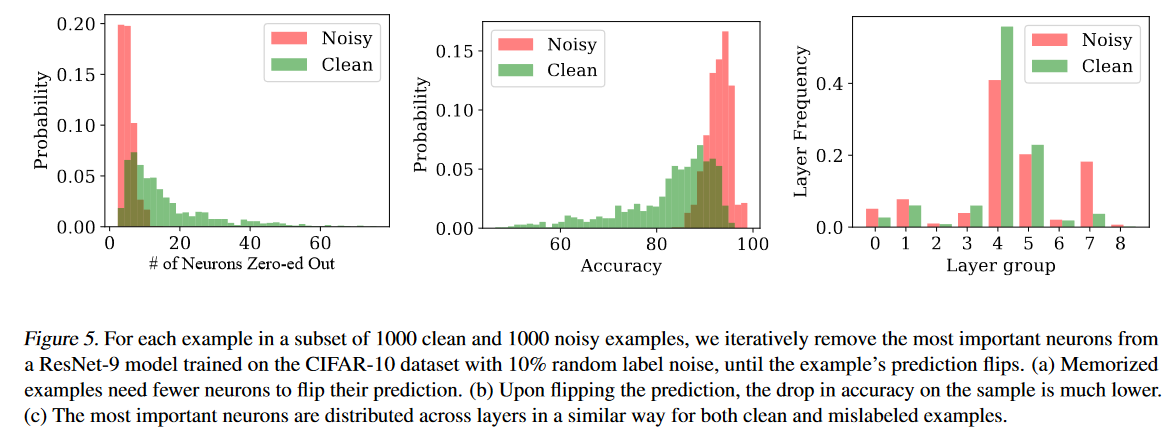

论文将对样本重要的神经元屏蔽，并计算剩余训练样本在模型上的准确率。结果发现记忆噪声样本的神经元对总体准确率的影响远小于记忆干净样本的神经元，且屏蔽噪声样本的神经元比屏蔽干净样本的神经元的准确率高10%

此外，观察关键神经元的分布情况可以发现，关键神经元并没有分布在特定层。干净样本和记忆化样本的重要是神经元可能往往属于相似的层，而不是来自专门的层。可能有某些层对模型整体很重要。关键神经元分散在多个层说明记忆并不局限于特定的层，而是多个神经元共同负责。

未来研究可以利用关键神经元移除作为检测噪声样本的方法（噪声样本的关键神经元较少）。使用这种方法检测错误标注样本的效果优于现有方法。

2.4.2 样本绑定dropout：对特定神经元进行定向记忆

根据前面的观察，正确预测错误标记的样本所需的信息通常比干净样本所需的信息要少得多。更有趣的是，通过将干净样本的预测通过归零个别激活来改变，通常会显著增加模型在同一训练集和测试集上的整体准确性损失。这些发现促使尝试将样本的记忆化过程引导到事先固定的神经元上。

为了实现将神经元子集与每个样本连接的想法，我们为每层分配一个固定比例的神经元（记为pgen），这些神经元永远不会被丢弃。我们将这些神经元称为泛化神经元。在卷积层的情况下，为了保持通道结构，我们同样选择一个固定比例的通道（记为pgen），这些通道永远不会被丢弃。在剩余的部分中，我们为每个样本分配一个小子集的pmem神经元，这些神经元在采样特定样本时会被激活。目标是将所有特征学习引导到pgen神经元集合上，并将与样本特定记忆化相关的神经元引导到pmem神经元集合上。在测试时，我们会丢弃对应于pmem的神经元，即将其激活归零，从而调整模型，使得可以去除记忆化的影响。

样本绑定丢弃的实验表明，确实可以将样本的记忆化限制在预先确定的神经元集合中。在ResNet 9模型的每一层后，我们添加一层“样本绑定丢弃”，并在MNIST、SVHN和CIFAR10数据集上进行训练，训练设置中有10%的均匀随机标签噪声。在丢弃记忆化神经元后，三个数据集的错误标记样本的准确率分别降至0.1%、1.4%和3.1%，尽管模型在训练时几乎完美拟合了所有的噪声数据。在所有情况下，对干净样本的有效影响分别为0.8%、4.2%和9.2%，同时降低了训练和测试性能之间的泛化差距。这表明，pgen比例的（泛化）神经元已经包含了分类数据集原型样本所需的特征。

为了理解在移除记忆化神经元后，干净样本准确率下降的原因，我们发现，大多数模型不再正确预测的样本实际上要么是标记错误和模糊不清的样本，要么是数据集中具有例外性和独特性的样本，模型必须记忆这些样本才能正确预测（见下图）。

为了评估pgen和pmem的取值对样本绑定丢弃方法在神经元中定位记忆化的能力的影响，我们在12种不同的参数组合上进行了网格搜索。表2展示了这些值变化对方法有效性变化的结果。我们发现，该方法对pgen和pmem的广泛取值（和组合）具有鲁棒性。一般来说，我们观察到一个趋势：随着泛化神经元容量的增加，记忆化神经元中的记忆化定位持续减少（即，在丢弃记忆化神经元后，噪声样本的准确率提高）。与此同时，这也导致了在丢弃记忆化神经元后，干净样本准确率的提高。

和其它baseline的对比测试：对于给定的pgen值，我们选择两个等效的模型：（a）使用标准丢弃法，p = pgen；（b）使用稀疏网络，剩余参数比例 = pgen。然后，我们最终比较在CIFAR-10数据集上训练50个epoch后，模型在干净样本和噪声样本上的准确率，使用ResNet-9模型。在样本绑定丢弃的情况下，我们丢弃记忆化神经元，同时在表3中测量准确率。我们发现，在相同的稀疏性水平下，当样本绑定丢弃能够将记忆化引导到选定的神经元集时，稀疏和标准丢弃方法仍然能够过拟合训练集（包括错误标记的样本）。

3. 结论和收获

巧思的实验设计，严谨的论证过程，规范的行文结构。